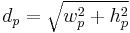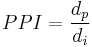Pixel density
Pixels per inch (PPI) or pixel density is a measurement of the resolution of devices in various contexts; typically computer displays, image scanners, and digital camera image sensors.
PPI can also describe the resolution, in pixels, of an image to be printed within a specified space. Note, the unit is not square inches. For instance, a 100×100 pixel image that is printed in a 1-inch square has a resolution of 100 pixels per inch (PPI). Used in this way, the measurement is meaningful when printing an image. Good quality photographs usually require 300 pixels per inch when printed.
Contents |
Computer displays
The PPI of a computer display is related to the size of the display in inches and the total number of pixels in the horizontal and vertical directions. This measurement is often referred to as dots per inch, though that measurement more accurately refers to the resolution of a computer printer.
For example, a 15 inch (38 cm) display whose dimensions work out to 12 inches (30.48 cm) wide by 9 inches (22.86 cm) high, capable of a maximum 1024×768 (or XGA) pixel resolution, can display around 85 PPI in both the horizontal and vertical directions. This figure is determined by dividing the width (or height) of the display area in pixels by the width (or height) of the display area in inches. It is possible for a display’s horizontal and vertical PPI measurements to be different (e.g., a typical 4:3 ratio CRT monitor showing a 1280×1024 mode computer display at maximum size, which is a 5:4 ratio, not quite the same as 4:3). The apparent PPI of a monitor depends upon the screen resolution (that is, the number of pixels) and the size of the screen in use; a monitor in 800×600 mode has a lower PPI than does the same monitor in a 1024×768 or 1280×960 mode.
The dot pitch of a computer display determines the absolute limit of possible pixel density. Typical circa-2000 cathode ray tube or LCD computer displays range from 67 to 130 PPI.
The IBM T220/T221 LCD monitors marketed from 2001 to 2005 reached 204 PPI.
The Toshiba Portégé G900 Windows Mobile 6 Professional phone, launched in mid 2007, came with a 3" WVGA LCD having “print-quality” pixel density of 313 PPI.[1]
In January 2008, Kopin Corp. announced a 0.44 inch (1.12 cm) SVGA LCD with an astonishing pixel density of 2272 PPI (each pixel only 11¼ μm).[2][3] According to the manufacturer, the LCD was designed to be optically magnified to yield a vivid image and therefore expected to find use in high-resolution eye-wear devices.
It has been observed that the unaided human eye can generally not differentiate detail beyond 300 PPI;[4] however, this figure depends both on the distance between viewer and image, and the viewer’s visual acuity. Modern displays having upwards of 300 PPI pixel densities, combined with their non-reflective, bright, evenly lit and interactive display areas, may have vastly more appeal to users than the best prints available on paper. Such high pixel density display technologies would make supersampled antialiasing obsolete, enable true WYSIWYG graphics and, further, pave the way towards the elusive “paperless office” era.[5] For perspective, such a device at 15 inch (38 cm) screen size would have to display more than four Full HD screens (or WQUXGA resolution).
The PPI pixel density specification of a display is also useful for calibrating a monitor with a printer. Software can use the PPI measurement to display a document at “actual size” on the screen.
Calculation of monitor PPI
Theoretically, PPI can be calculated from knowing the diagonal size of the screen in inches and the resolution in pixels (width and height). This can be done in two steps:
1. Calculate diagonal resolution in pixels using the Pythagorean theorem:
2. Calculate PPI:
where
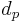 is diagonal resolution in pixels,
is diagonal resolution in pixels,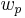 is width resolution in pixels,
is width resolution in pixels,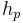 is height resolution in pixels and
is height resolution in pixels and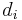 is diagonal size in inches. (This is the number advertised as the size of the display.)
is diagonal size in inches. (This is the number advertised as the size of the display.)
For example, for a 20 inch (50.8 cm) screen with a 1680×1050 resolution (in which 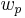 = 1680,
= 1680, 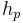 = 1050 and
= 1050 and 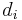 = 20), we get 99.06 PPI; for a typical 10.1 inch netbook screen with a 1024×600 resolution (in which
= 20), we get 99.06 PPI; for a typical 10.1 inch netbook screen with a 1024×600 resolution (in which 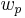 = 1024,
= 1024, 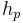 = 600 and
= 600 and 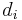 = 10.1), we get 118 PPI.
= 10.1), we get 118 PPI.
Note that these calculations are not very precise. Frequently, screens advertised as “X inch screen” can have their real physical dimensions of viewable area differ, for example:
- HP LP2065 20 inch (50.8 cm) monitor — 20.1 inch (51 cm) viewable area[6]
Calculating PPI of camera screens
Camera manufacturers often quote camera screens in 'number of dots'. This is not the same as the number of pixels. There are 3 'dots' per pixel, red, green and blue. For example, the Canon 50d is quoted as having 920,000 dots.[7] This translates as 307,200 pixels (x3 = 921,600 dots). This translates to the screen actually being 640×480[8]
This must be taken into account when working out the PPI. Using the above calculations, you require the screen's dimensions, but other methods require you to have the total pixels, not total dots.
'Dots' and 'pixels' are often confused in reviews and specs when viewing information about digital cameras specifically.
Scanners and cameras
"PPI" or "pixel density" may also be used to describe the resolution of an image scanner. In this context, PPI is synonymous with samples per inch.
In digital photography, pixel density is the number of pixels divided by the area of the sensor. A typical DSLR circa 2011 will have 1-4,5 MP/cm2; a typical compact will have 20-60 MP/cm2. For example Sony Alpha 55 has 16.2 megapixels on an APS-C sensor having 4,5 MP/cm2 since a compact camera like Sony Cybershot DSC-H70 has 16.2 megapixels on an 1/2.3" sensor having 60 MP/cm2. Interestingly, as can be seen here, the professional camera has a lower PPI than does a compact, because it has larger photodiodes due to having far larger sensors.
Metrication
The digital publishing industry often uses "pixels per centimeter" instead of "pixels per inch".[9][10][11] This is because all countries in the world except three use the metric system.
See also
- List of displays by pixel density
- Dots per inch
- Computer monitor DPI standards - the origins of 96 DPI/PPI as Microsoft/Windows standard and 72 DPI/PPI as (former) Apple/Macintosh standard
- Dot pitch
- Resolution independence
References
- ^ "Toshiba Portégé G900 Official Page". Toshiba Portege G900 Review. 2007-07-27. http://www.toshiba-europe.com/mobile/Mobile2Live.aspx?WCI=PageNavigate&WCE=&WCU=%3bLANG%3d1%3bPID%3d165%3bTYP%3d18%3bPNT%3d0%3bSEC%3d2. Retrieved 2008-05-01.
- ^ "Kopin unveils smallest color SVGA display". optics.org. 2008-01-11. http://optics.org/cws/article/industry/32411. Retrieved 2008-06-06.
- ^ "Company Debuts World’s Smallest Color SVGA Display". SID, Information Display magazine May 2008 Vol. 24, No. 05. 2008-05-31. http://www.kopin.com/data/Mar%2008%20Med%20Products%20Manu.pdf. Retrieved 2008-06-06.
- ^ "Apple Retina Display". Jonesblog. 2010-06-24. http://prometheus.med.utah.edu/~bwjones/2010/06/apple-retina-display/. Retrieved 2011-09-25.
- ^ "Electronic displays for information technology". IBM Journal of Research and Development Volume 44, Number 3, 2000. 1999-11-10. http://www.research.ibm.com/journal/rd/443/wisnieff.html. Retrieved 2008-06-06.
- ^ HP LP2065 20-inch (50.8 cm) LCD Monitor - Specifications and Warranty (Hewlett-Packard Company official website)
- ^ dpreview.com, Canon EOS 50d
- ^ Techcrunch.com, dots vs pixels
- ^ "Web Graphics Basics". http://www.washington.edu/accessit/webdesign/student/unit4/module2/web_graphics_basics.htm.
- ^ "Utads.com Glossary of Terms". http://www.utads.com/ad_specs/glossary.html.
- ^ "Resolution, dpi and ppi". http://www.monarda.se/extra/ppi-test/ppitest_english.htm.
External links
- A very nice graphical PPI ruler - works even if you have just a piece of office paper
- Easy to use monitor DPI/PPI calculator, includes dot pitch
- Free on screen pixel ruler for Windows
- A ruler-based graphical pixel size/density measurement tool
- Nice looking online monitor DPI (or PPI or pixel-density) calculator with automatic resolution detection